 Laboratório de Ensino de Matemática
Laboratório de Ensino de Matemática
Links
- 1.
- Com hexágonos regulares é possível "ladrilhar" o plano
- 2.
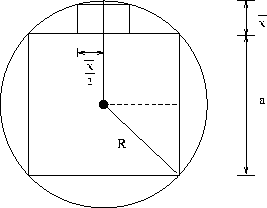
- Dentre as figuras que "ladrilham" o plano, o hexágono é o
"melhor"
Dentre os polígonos regulares de mesmo perímetro é o
que maximiza a área; ou
Dentre os polígonos regulares de mesma área é o
que minimiza o perímetro;
- Introdução de Séries a partir de problemas concretos e interessantes
- Testes: no computador
- Caso I: Demonstrações -> trabalhar com áreas
- Como processo de contagem


- Relações entre as duas séries:
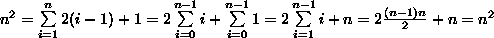
- Caso II: Demonstrações -> construção ou indução
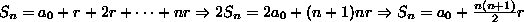
- Como problema de divisão de uma barra de chocolate
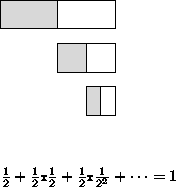
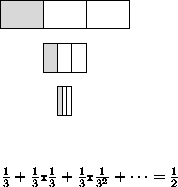
- Demonstração: construção ou indução
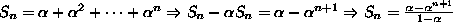
Exemplos (1) (2) (3) (4) (5) (6) (7)
Existe alguma boa razão para que um favo de abelhas seja formado por formas hexagonais?

Conjectura:
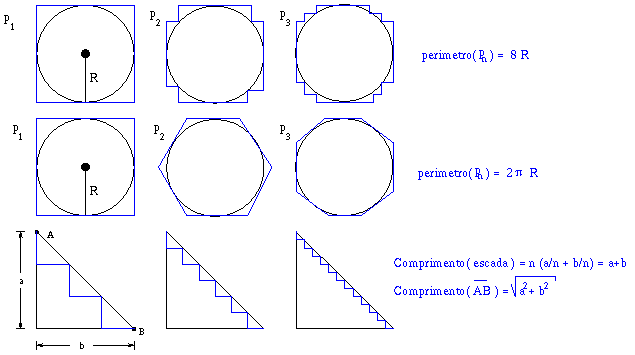
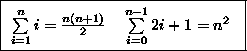 |
|
I: Série com problema de contagem | II: Série a partir de um problema visualmente atrativo (fractal) ou através de um interessante Falso-Paradoxo (Aquiles e a Tartaruga) (siga o "link" para ver os exemplos motivadores) |
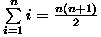 e
e 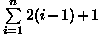 ,
mas como encontrar a expressão ("fórmula fechada") para uma série
genérica, digamos
,
mas como encontrar a expressão ("fórmula fechada") para uma série
genérica, digamos
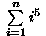 ?
?
Se a série tem como "fórmula fechada" um polinômio (como é o caso de toda série com termo ik), então é possível usar interpolação para obter esta fórmula. Uma maneira de fazer isto é via sistemas lineares (siga o "link" para ver como isto é feito).
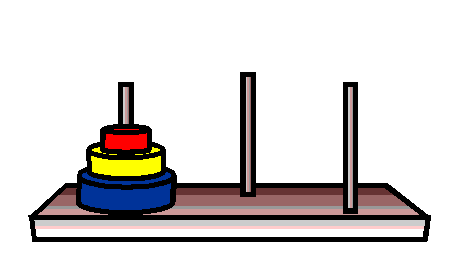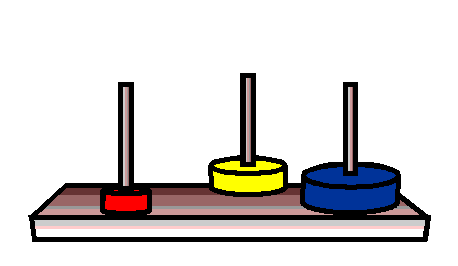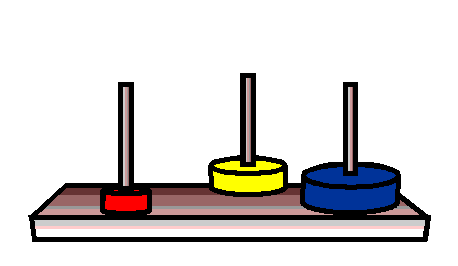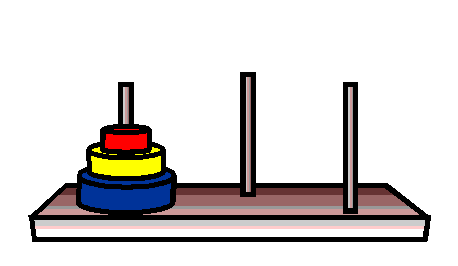
Existe uma lenda associada a este problema, resumidamente: o mundo vai
acabar quando esta tarefa for terminada.
Experimente uma versão interativa do jogo
clicando aqui.